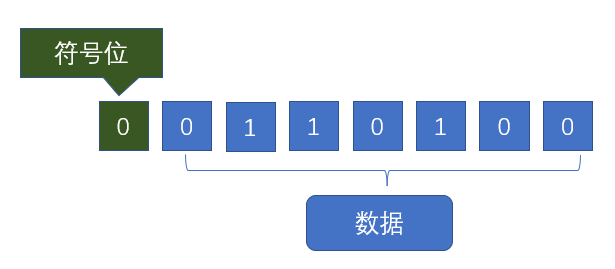
一个数在计算机中的表示形式是二进制,这个数其实就叫机器数。机器数是带符号的,在计算机用一个数的最高位存放符号,正数为0, 负数为1。
原码
十进制数据的二进制表现形式,最左边是符号位,0为正,1为负。
我们拿一个字节来讲,一个字节的长度是8个比特位
所以对于一个来讲最大的数字就是01111111换成十进制就是127,那么最小数是多少呢?负数的符号位为1,所以最小数应该是10000000,对吗?
转换10进制后结果是-0,怎么能使最小数呢,所以最小数应该是11111111,转换为10进制就是-127,这才是一个字节所能表达的最小数(此处不接受反驳,具体后面会讲)
使用原码进行计算
正数计算
我们测试使用正数二进制原码对其0依次加至5,发现计算的结果转为10进制是正确的。

利用原码对正数进行计算是不会有问题的
负数计算
我们先对-0进行+1计算,得到结果为-1,实际应该为1
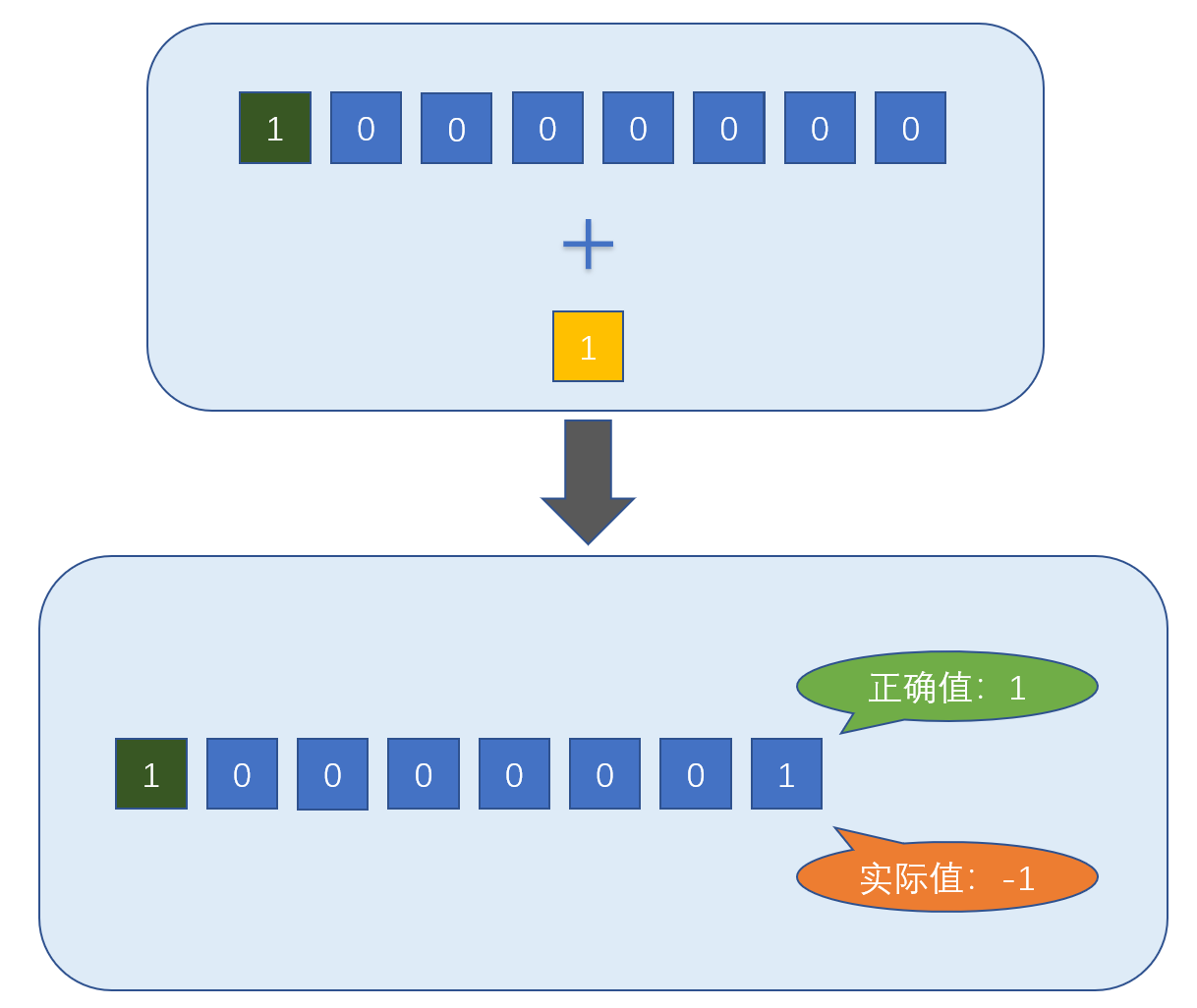
我们在-1的基础上,对其进行+1计算,原则上-1+1应该等于0,实际却等于-2
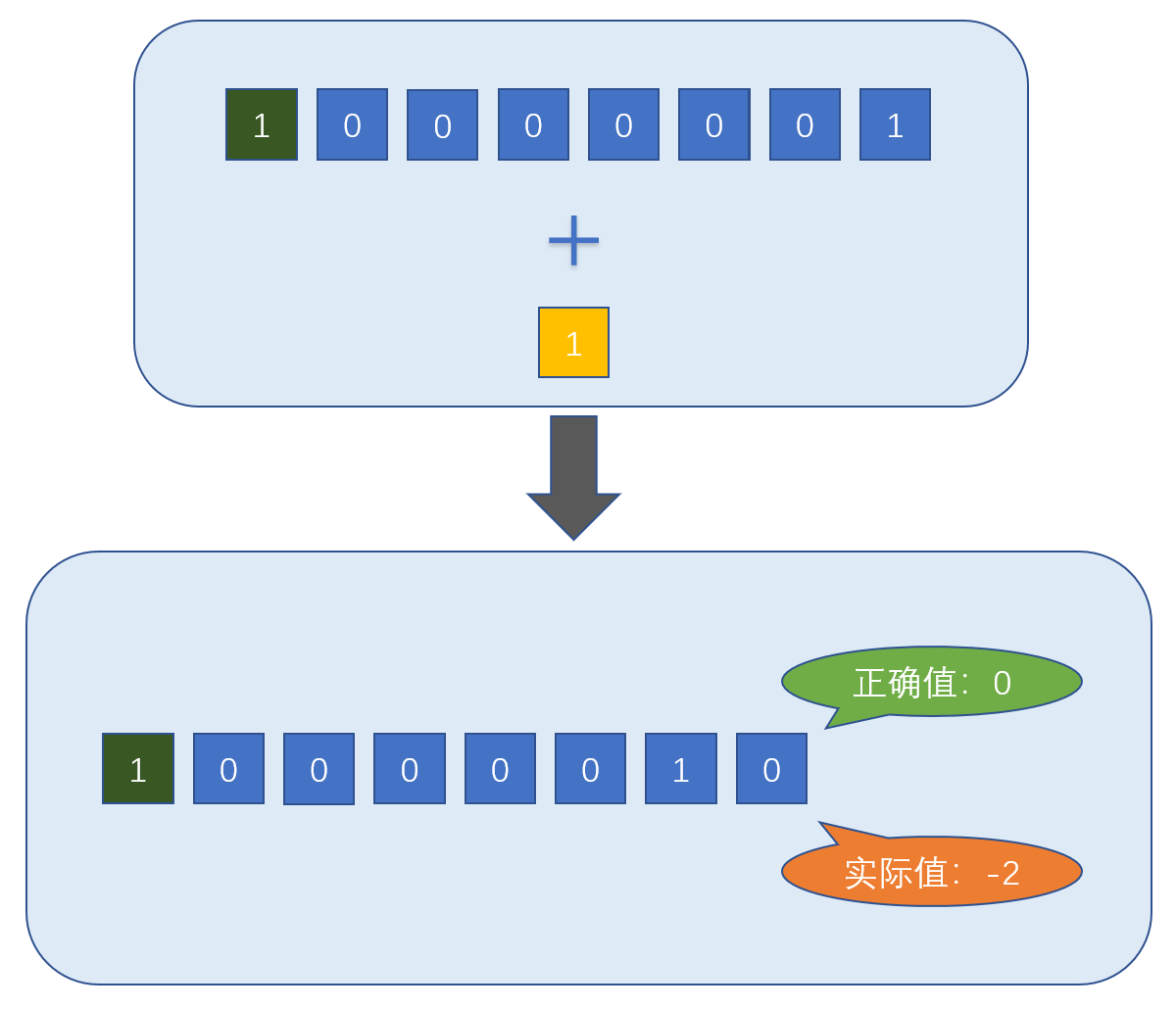
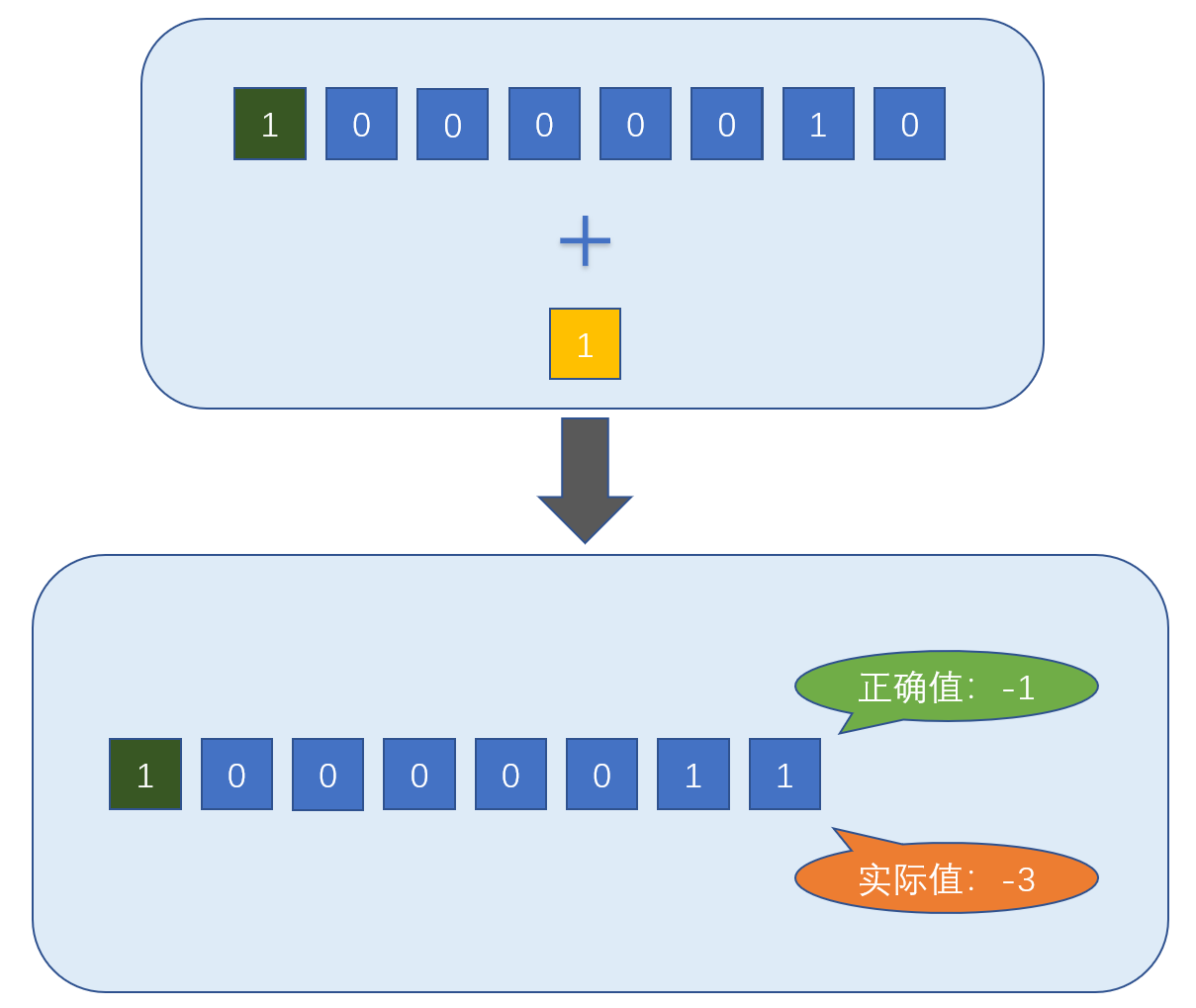
如果你还没看懂,那我们继续演示,我们在-2的基础上,对其进行+1计算,原则上-2+1应该等于-1,实际却等于-3
拿之前我们上学的时候学的数轴来说明,负数进行相加,往数轴反反向进行了计算,大概如下:
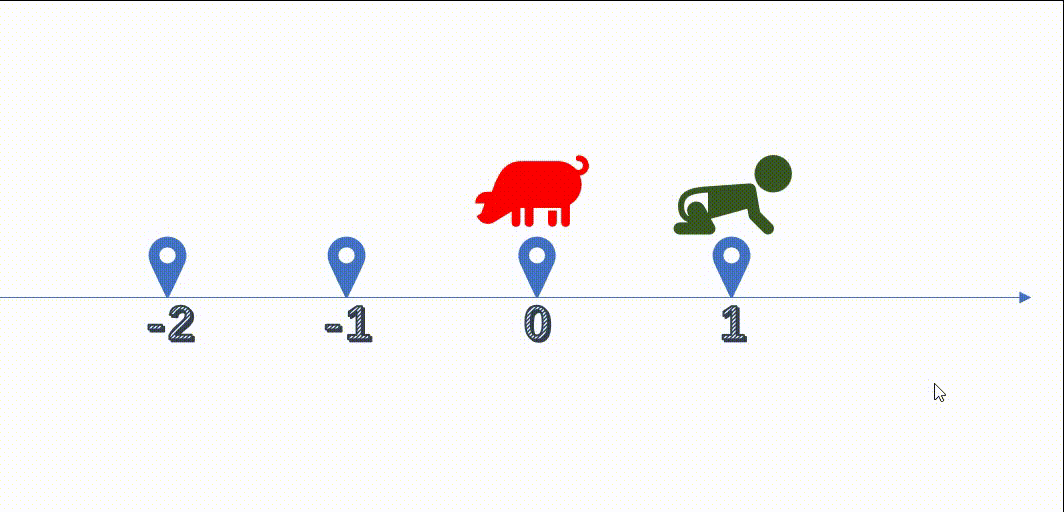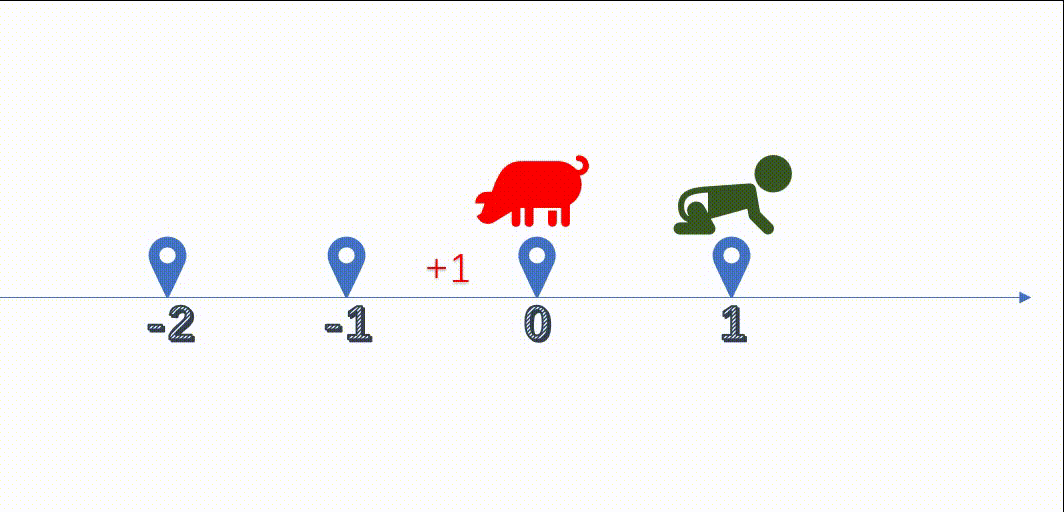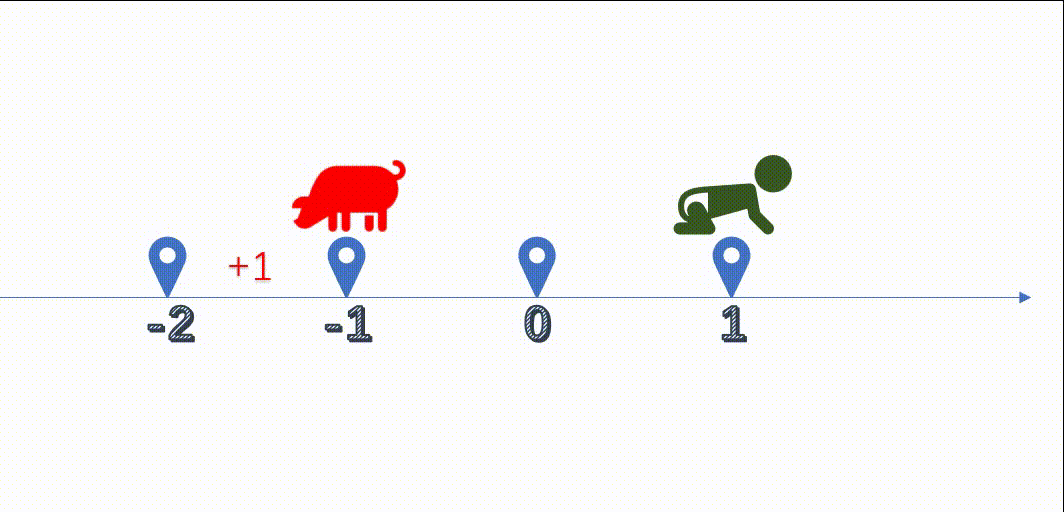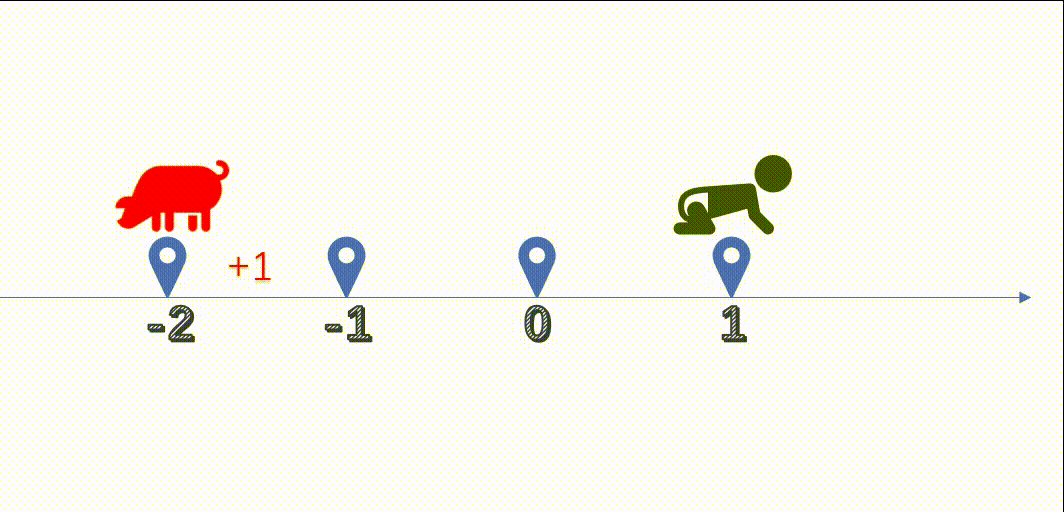
如果是负数计算,结果就会出错,实际运算的结果,跟我们预期的结果是相反的。
我们可能会想了,那我们把数轴方向旋转180度,换个方向不就可以了吗?酷,于是就出现了反码。
反码
正数的反码、补码是其本身,负数的反码是符号位保持不变,其余位取反
对于正数,它的反码就是其原码(原码和反码相同);负数的反码是将原码中除符号位以外的所有位(数值位)取反,也就是 0 变成 1,1 变成 0。
反码是为了解决不能计算负数的问题而出现的。
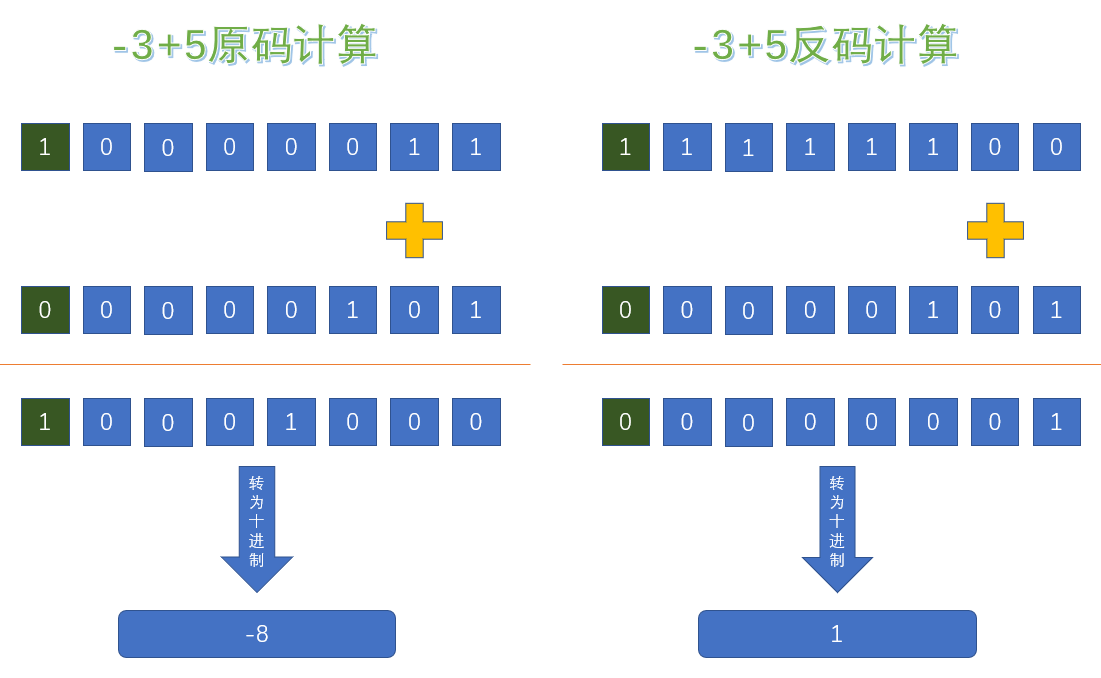
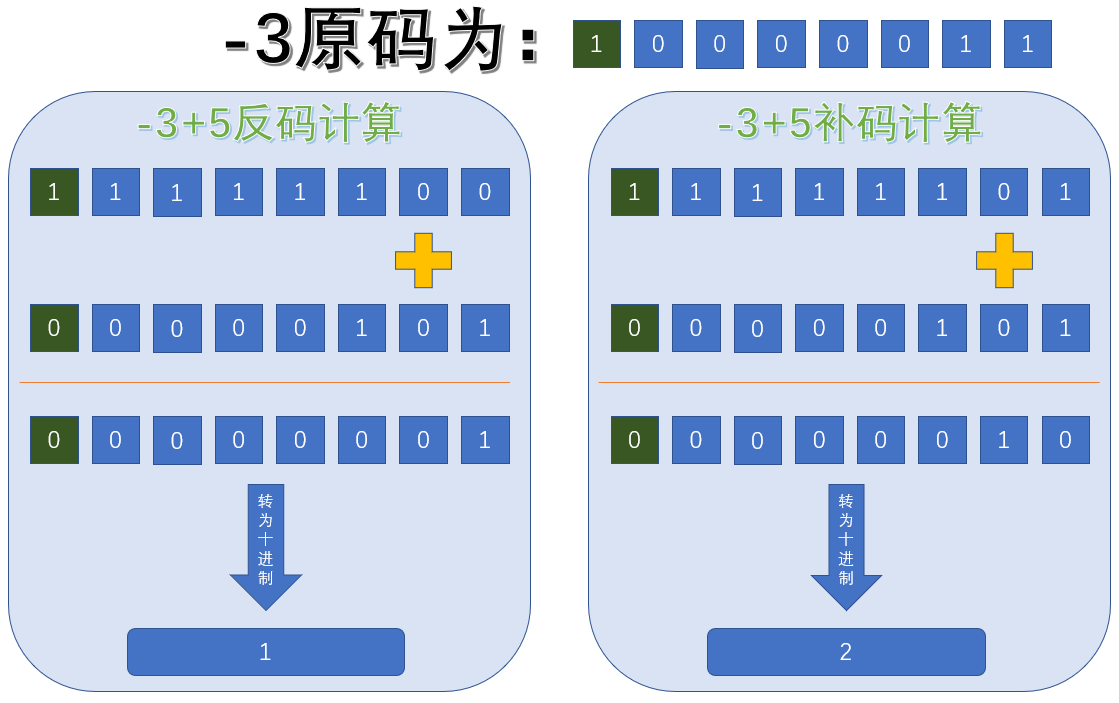
下例中我们计算-56+1,使用原码计算结果得出-57,真是逗小学生呢;
我们采用-56反码进行计算,结果再转为原码,结果得出-55,这才乖嘛。

你以为就结束了?结束了干嘛又弄个补码呢?我们再举个例子
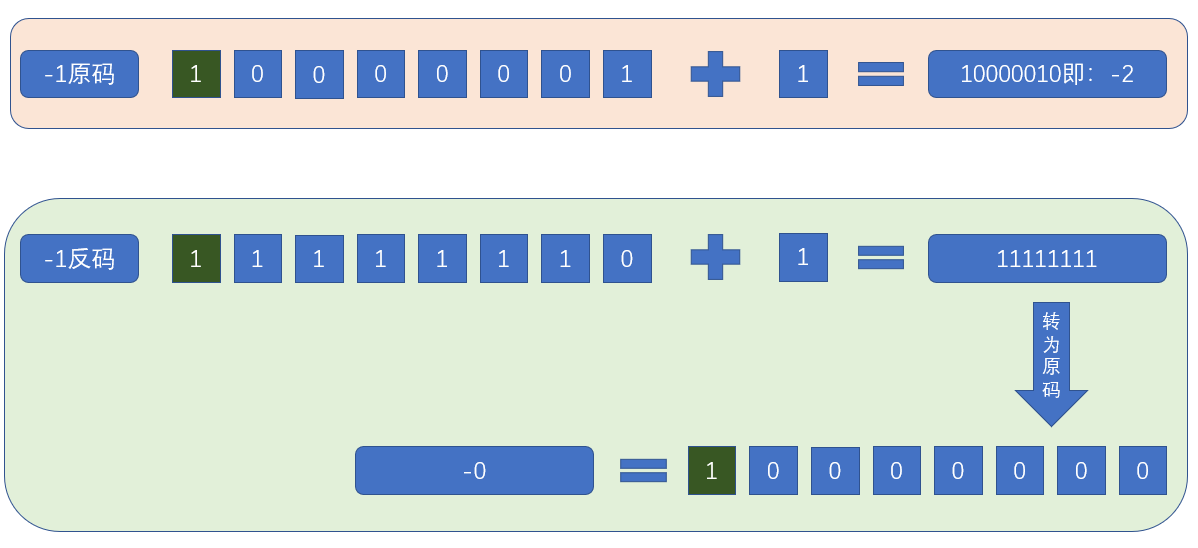
-1使用反码计算不是一样可以得到正确答案嘛,是的
-0呢?敢不敢跟老夫再走一遭?
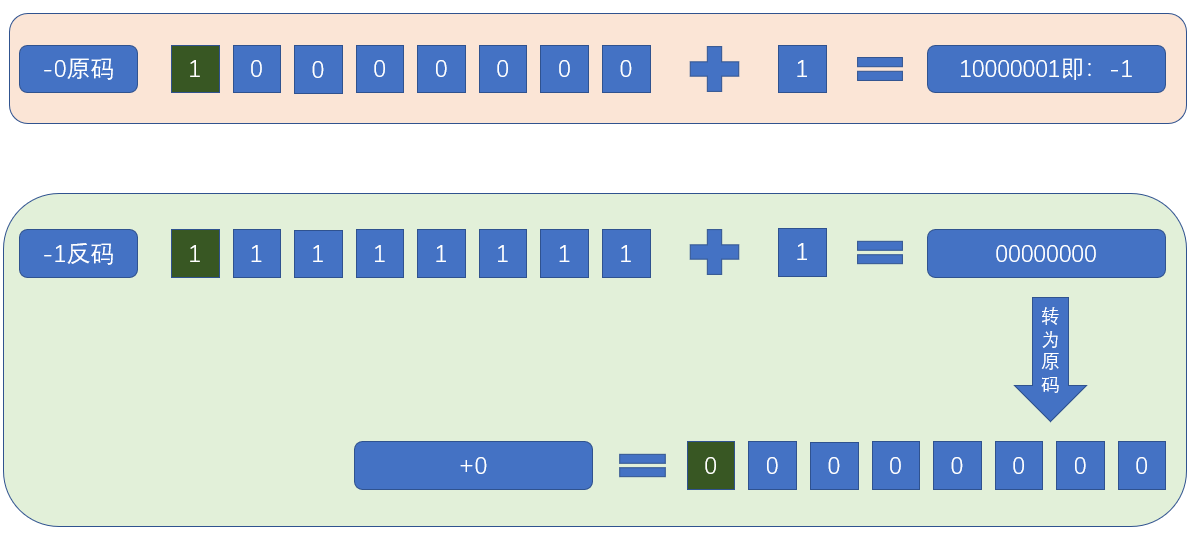
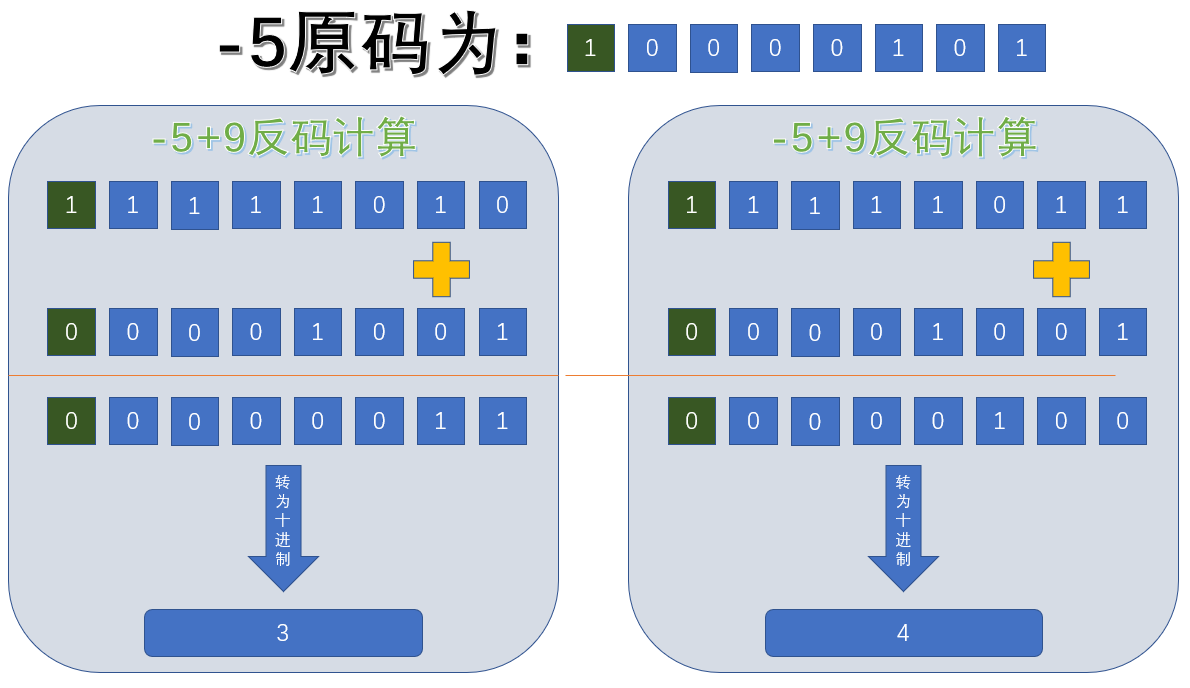
上述使用原码计算有问题我们都知道,直接看反码的计算,11111111+1=100000000,但是我们刚开始就说了,我们讲的是1个字节的计算,所以只考虑8位,超出8个比特位的直接舍去,所以结果就是00000000,第一位是0,也就是正数了,正0。
产生这种误差的原因就是因为,在反码中,0的表示形式有两种:10000000和00000000,所以进行夸0计算时,就会产生这种误差,不信我再来一例。
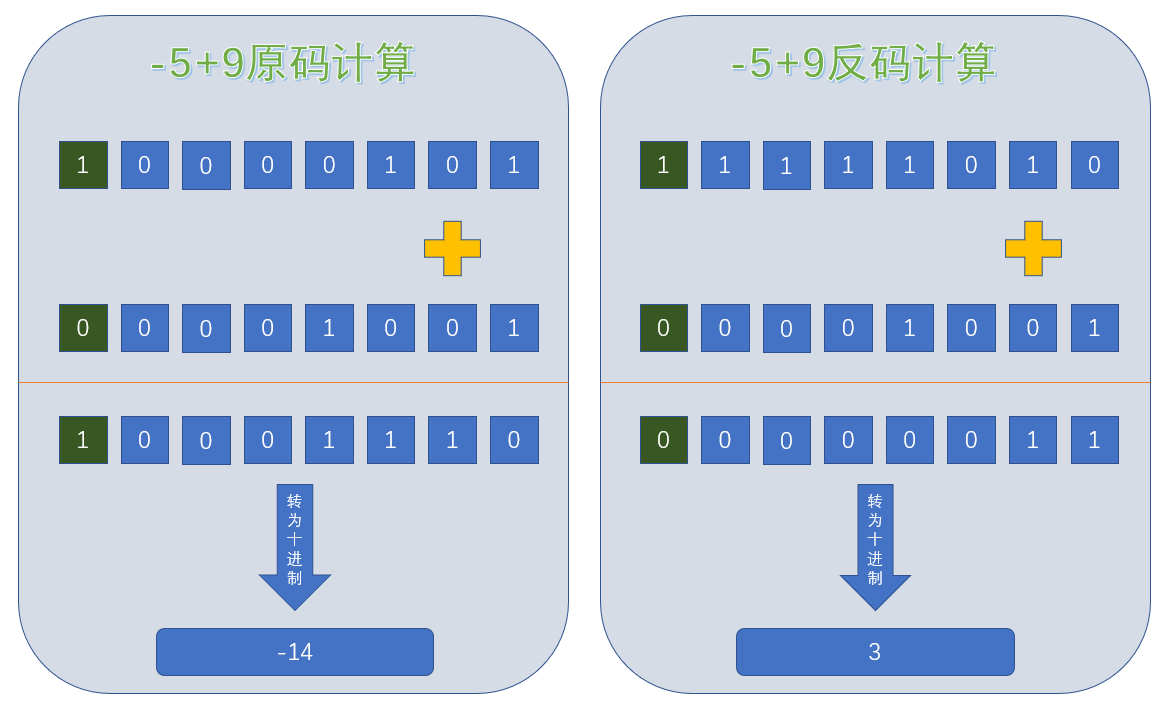
上述示例来看,使用反码只要是跨0的计算,结果都跟正确结果差了1,这就是反码计算时0的两种表现形式导致的,为了解决这个问题,当当当当,补码出现了。
补码
对于正数,它的补码就是其原码(原码、反码、补码都相同);负数的补码是其反码的基础上加 1。
可以认为,补码是在反码的基础上打了一个补丁,进行了一下修正,所以叫“补码”。
补码出现的目的就是为了解决负数计算时跨0的问题而出现的;
补码的计算规则
正数的补码不变,负数的补码在反码的基础上+1;
另外补码还能多记录一个特殊的值-128,该数据在1个字节下,没有原码和反码。
注:计算机中的存储和计算都是以补码的形式进行的
示例:
补码到底是如何简化硬件电路的
由于整数在内存中是以补码表示的,那么计算机只要设计一种简单的、不用区分符号位和数值位的加法电路,就能同时实现加法和减法运算,并且非常高效,极大简化了计算机的硬件电路
下面演示了按照补码计算的过程:
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 | 6 – 18 = 6 + (-18) = [0000 0000 0000 0110]补 + [1111 1111 1110 1110]补 = [1111 1111 1111 0100]补 = [1111 1111 1111 0011]反 = [1000 0000 0000 1100]原 = -12 18 – 6 = 18 + (-6) = [0000 0000 0001 0010]补 + [1111 1111 1111 1010]补 = [1 0000 0000 0000 1100]补 = [0000 0000 0000 1100]补 = [0000 0000 0000 1100]反 = [0000 0000 0000 1100]原 = 12 5 – 13 = 5 + (-13) = [0000 0000 0000 0101]补 + [1111 1111 1111 0011]补 = [1111 1111 1111 1000]补 = [1111 1111 1111 0111]反 = [1000 0000 0000 1000]原 = -8 13 – 5 = 13 + (-5) = [0000 0000 0000 1101]补 + [1111 1111 1111 1011]补 = [1 0000 0000 0000 1000]补 = [0000 0000 0000 1000]补 = [0000 0000 0000 1000]反 = [0000 0000 0000 1000]原 = 8 |
总结
原码、反码、补码的概念只对负数有实际意义,对于正数,原码、反码、补码都是一样的。
在计算机内存中,整数一律采用补码的形式来存储。这意味着,当读取整数时还要采用逆向的转换,也就是将补码转换为原码。将补码转换为原码也很简单:先减去 1,再将数值位取反即可。
最后列出几个简单的数字原码、反码、补码对应表,大家对应着计算下,可以深刻理解这三个东西的由来
| 十进制 | 原码 | 反码 | 补码 |
|---|---|---|---|
| +0 | 00000000 | 00000000 | 00000000 |
| -0 | 10000000 | 11111111 | 00000000 |
| -1 | 10000001 | 11111110 | 11111111 |
| -2 | 10000010 | 11111101 | 11111110 |
| -3 | 10000011 | 11111100 | 11111101 |
| -4 | 10000100 | 11111011 | 11111100 |
| -5 | 10000101 | 11111010 | 11111011 |
| …… | …… | …… | …… |
| -127 | 11111111 | 10000000 | 10000001 |
| -128 | 无 | 无 | 10000000 |

